本篇目录:
左子树的根节点是什么意思
在计算机科学中,二叉树是每个结点最多有两个子树的树结构。通常子树被称作“左子树”和“右子树”,二叉树常被用于实现二叉查找树和二叉堆。有根二叉树还要满足根结点的度不大于2。
左子树就是以当前节点看,它的左子节点那一分支的子树,该子树以当前节点左子节点为根。右子树就是以当前节点看,它的右子节点那一分支的子树,该子树以当前节点右子节点为根。
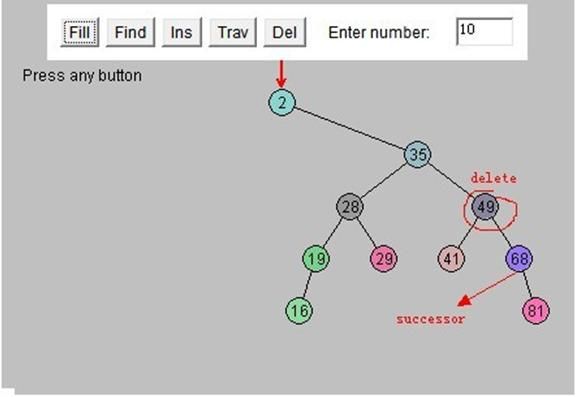
观察左子树ADEF,左子树的中的根节点必然是大树的root的leftchild。在前序遍历中,大树的rot的lefichild位于root之后,所以左子树的根节点为D。同样的道理,root的右子树节点HMZ中的根节点也可以通过前序遍历求得。
什么是满二叉树?节点又是什么?
1、满二叉树是二叉树的一种特殊情形。解析:满二叉树:如果一个二叉树的任何节点或者是树叶,或者恰有两棵非空子树,则此二叉树称为满二叉树。
2、完全二叉树的定义是一棵深度为k的有n个结点的二叉树,对树中的结点按从上至下、从左到右的顺序进行编号,如果编号为i(1≤i≤n)的结点与满二叉树中编号为i的结点在二叉树中的位置相同。

3、一棵深度为k,且有2^k-1个节点称之为满二叉树;深度为k,有n个节点的二叉树,当且仅当其每一个节点都与深度为k的满二叉树中,序号为1至n的节点对应时,称之为完全二叉树。
4、如果编号为i(1≤i≤n)的结点与满二叉树中编号为i的结点在二叉树中的位置相同。从满二叉树和完全二叉树的定义可以看出, 满二叉树是完全二叉树的特殊形态, 即如果一棵二叉树是满二叉树, 则它必定是完全二叉树。
5、完全二叉树的定义:深度为k,有n个结点的二叉树当且仅当其每一个结点都与深度为k的满二叉树中编号从1至n的结点一一对应时,称为完全二叉树。
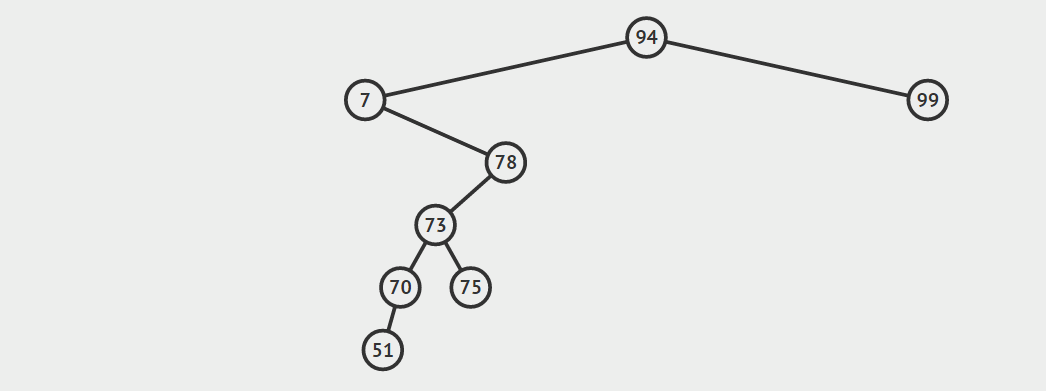
6、即如果一棵二叉树是满二叉树, 则它必定是完全二叉树。叶子结点不同 完全二叉树:完全二叉树的叶子结点可出现在最下层或次下层。满二叉树:满二叉树的叶子结点只能出现在最下层和次下层。
什么是叶子节点,度?根节点?
根节点是树的最顶端的节点,叶子结点是没有子结点的结点。根节点就是没有父节点只有子女节点的节点,是树的最顶端的节点,叶节点就是没有子女节点只有父节点的节点,又称为终端结点。
叶是叶节的缩写。叶子或叶子指的是网络结构中的计算机,它接收来自靠近中心的计算机而不是更远的计算机的信号。叶节点是树的底部段中的节点,叶节点不具有子节点。叶节点的结构比中间节点的结构稍微复杂一些。
叶子节点就是树中最底段的节点,叶子节点没有子节点。格式化叶子节点的结构比中间节点的结构稍微复杂一点。为了能够在一个格式化叶子节点中保存多个条目。
双亲节点也叫父节点,相对于当前的节点而言,它的上层节点就叫做父节点。当前节点下面已经没有其他任何节点了,当前的这个节点就叫做叶节点,是最底层的节点。
在层次模型中,数据库中有且仅有一个记录型无双亲,称为根节点;同一双亲的子结点称为兄弟结点;没有子结点的结点称为叶结点;代表两个记录型之间一对多的关系叫做双亲关系。
二叉树的度是指树中所以结点的度数的最大值。二叉树的度小于等于2,因为二叉树的定义要求二叉树中任意结点的度数(结点的分支数)小于等于2 ,并且两个子树有左右之分,顺序不可颠倒。
什么是节点?度?什么是二叉树?
1、节点:二叉树中每个元素都称为节点。度:二叉树的度表示节点的子树或直接继承者的数目,二叉树的度是一个子树或单子树。2度是两个孩子,或者左和右子树有两个叉树,最大度数为2。叶子:叶是叶节的缩写。
2、节点度就是这个节点的孩子数量,例如有左右孩子的节点,它的度为2,如果只有左孩子或者只有右孩子的节点,它的度就是1,叶节点就是度为0的节点(没有孩子)。先序遍历的话,只要孩子不是NULL,就可以将这个节点的度+1。
3、度=节点总数-1。在树中,每个节点有多少条边出去,该节点的度就为多少。也就是说,一条边贡献一个度。而树中,边的条数是节点数减去1。
4、在计算机科学中,二叉树是每个结点最多有两个子树的树结构。通常子树被称作“左子树”(left subtree)和“右子树”(right subtree)。二叉树常被用于实现二叉查找树和二叉堆。
5、二叉树的度是指树中所以结点的度数的最大值。二叉树的度小于等于2,因为二叉树的定义要求二叉树中任意结点的度数(结点的分支数)小于等于2。
到此,以上就是小编对于奈飞用哪个节点最好的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏